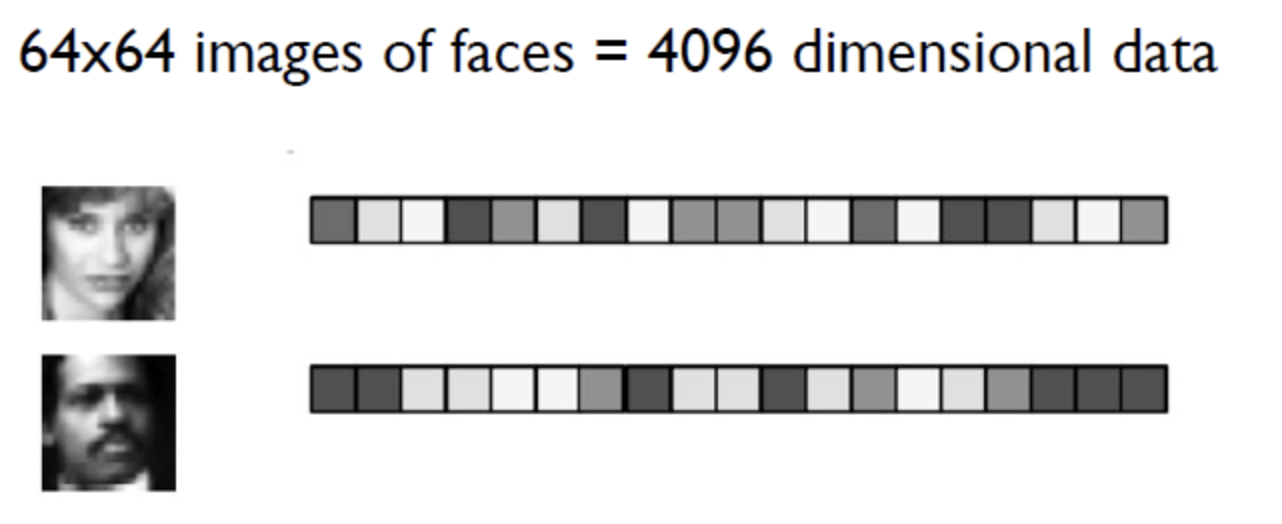PCA

Introduction §

Data is often high dimensional. So can’t be stored directly, nor ignored completely. Dimensionality reduction techniques are:

• [Filtering]: Leave most of the dimensions and concentrate only on certain dimensions
• [PCA]: Project the high-dimensional data onto a lower dimensional subspace using linear or non-linear transformations (or projections).

Info

The basic idea is n (the number of data items) should be more than number of dimensions.

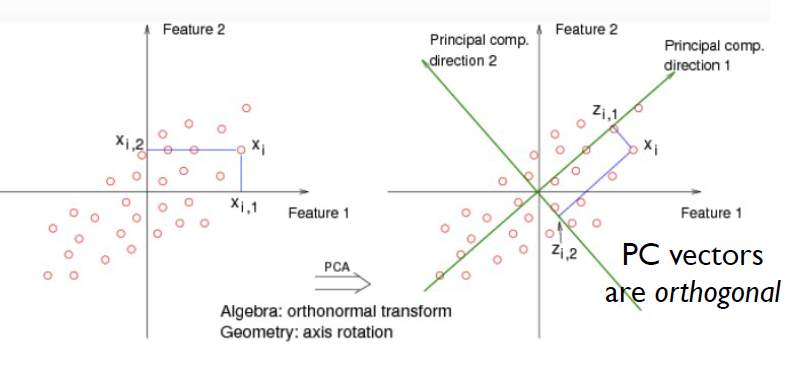
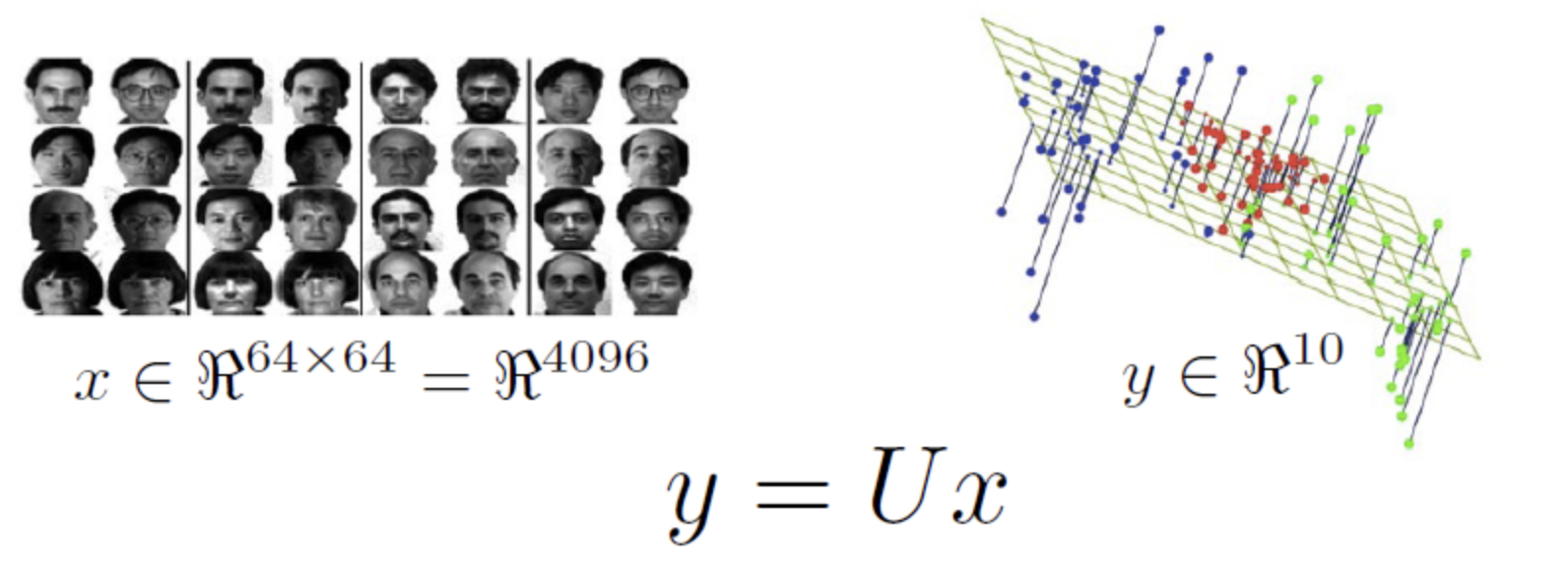The above is an example of PCA which is a linear projection method.

Detailed Explanation §

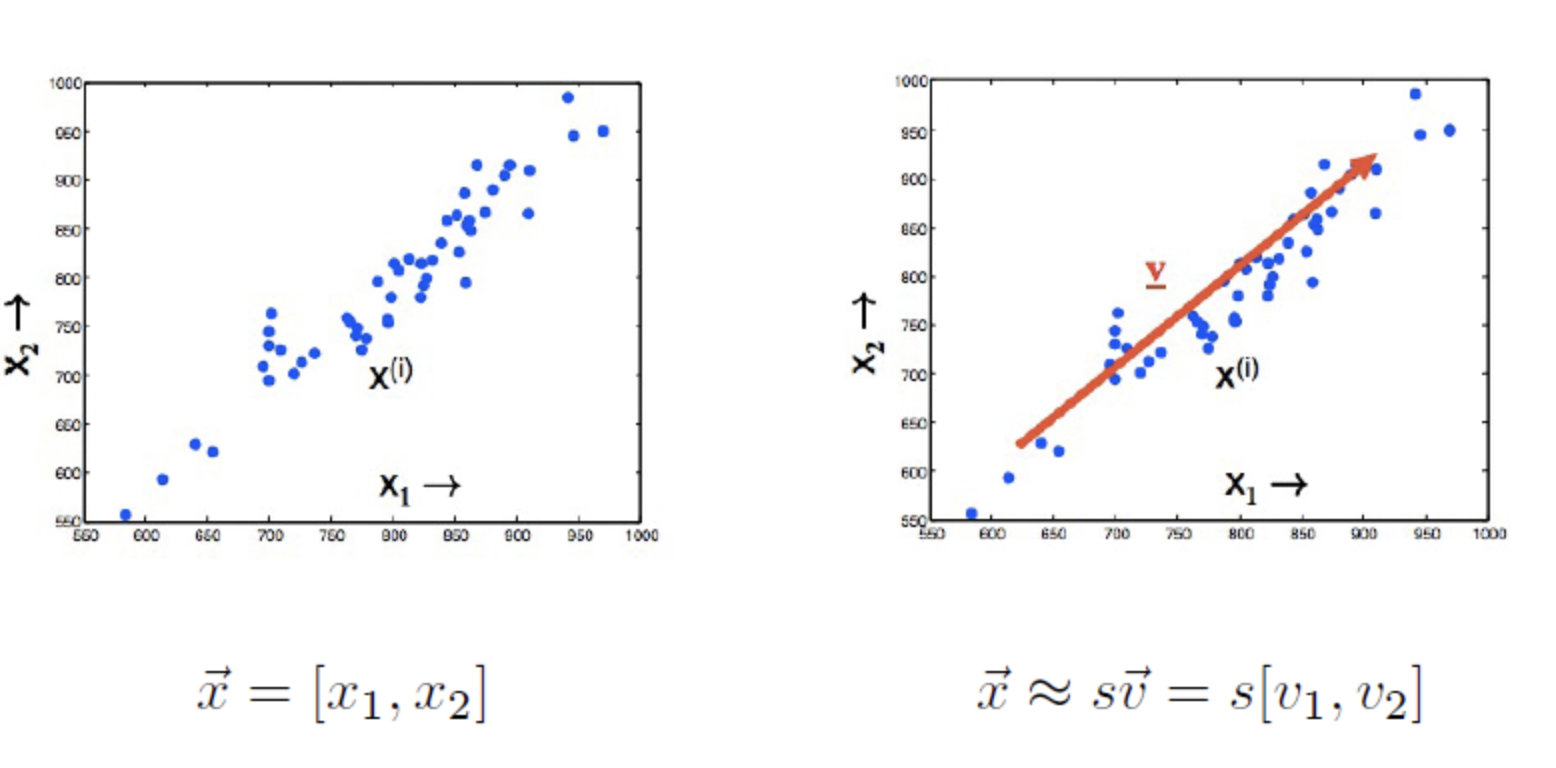
• Problem: Approximating 2-D datapoints using lower-dimensional representation, ie, 1-D
• Details:
  • Instead of storing 2 values for each data, we will store 1 value for each data plus vector V which is common across all the datapoints.
  • For each data point you have to store only this scalar value s, which gives the distance along this vector V.
• Other Details
  • You should choose V that will minimise the residual variance, ie, the difference b/w your original data and your projections.
  • It allows you to reconstruct the original data, with the least possible error.
  • Orthogonal projection on to the vector V.
  • You should pick V in the direction of biggest spread of your data.
  • Can extend this to multiple components.
  • you can repeat this process, and find second component that has second biggest variance of the data, ie, principal comp 2.

Understanding SVD §

Need for SVD

• The steps to implement PCA are expensive when X is very large or very small.
• Best way to compute principal components is by using SVD.
• SVD is one of the best linear transformation methods.

PCA Implementation

1. Subtract mean from the data.
2. Scale each dimensions by its variance.
3. Compute the covariance matrix S. Here X is data matrix. $S=1/N(X^{T}X)$
4. Compute K largest eigen vectors of S. These eigen vectors are the principal components of the data set.

What is SVD? §

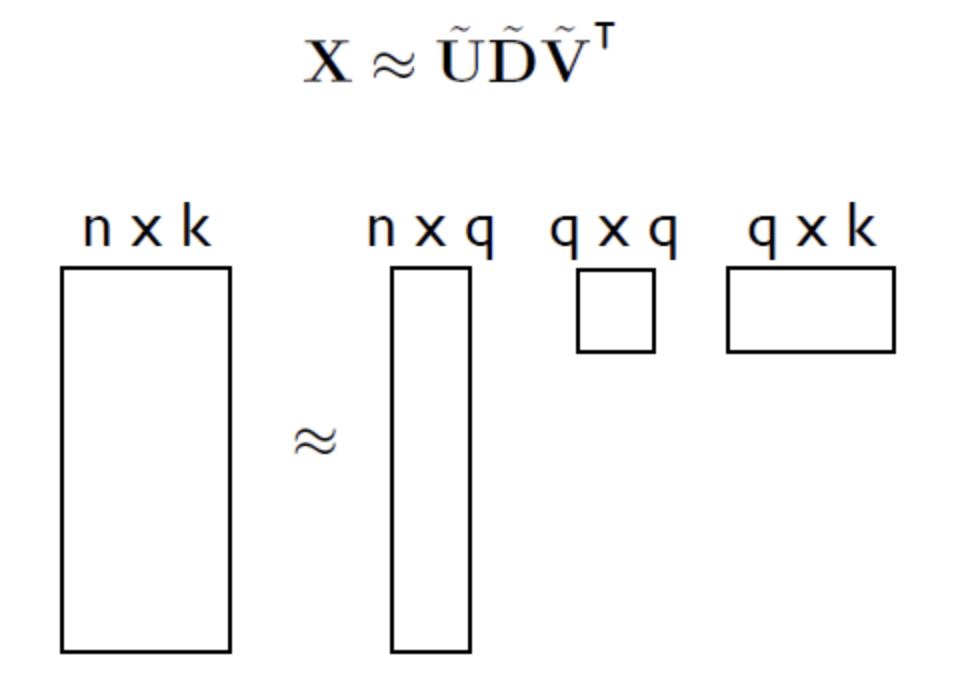
Any matrix X, whether it is singular, square or diagonal, can be decomposed into product of three matrices; two orthogonal matrices U and V and diagonal matrix D.

$X=UD{V}^T$

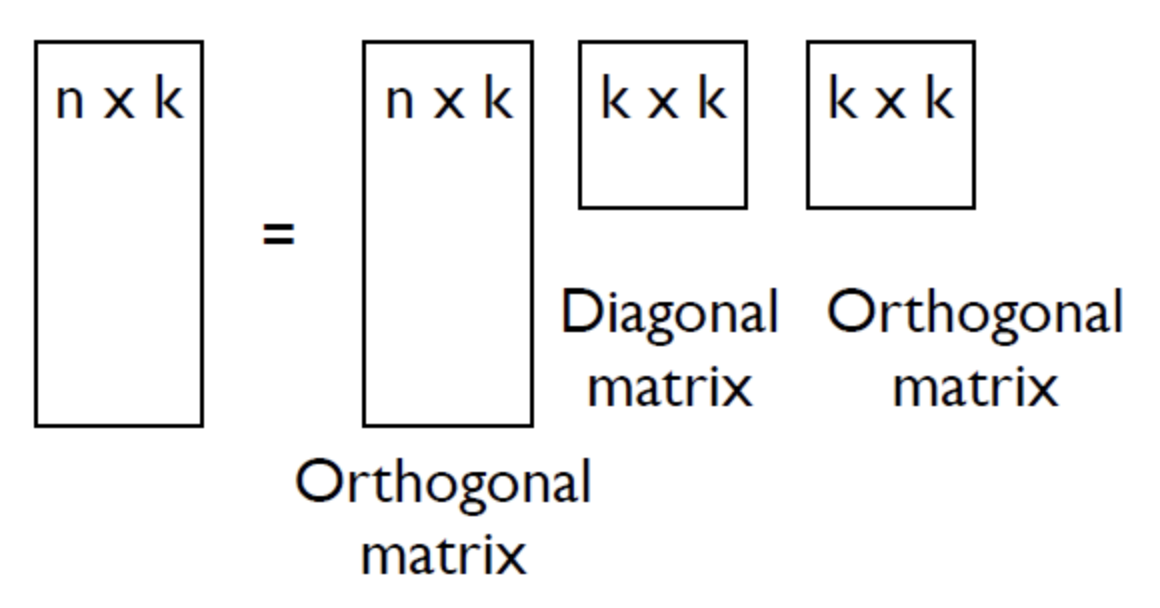
[PCA using SVD] on S(co-variance matrix) is used to obtain eigen vectors and eigen values.

• The columns of matrix U form the eigen vectors of S
• The D matrix is a diagonal matrix, whose diagonal values are eigen values in descending order.
• The eigen vectors have the same dimensions of a single datapoint.
• What does SVD has to do with Dimensionality Reduction?
  • How PCA helps in dimensionality reduction?
  • If we reduce number of dimensions from k to q (q < k).
  • Number of column vectors of U would have been changed to q, ie, we are now is q-dimensional hyper-plane in a k-dimensional world.

Intuition behind PCA using SVD Dimensionality Reduction

When we reduce the dimensions from k to q (q < k), then the points are now in q-dimensional hyper-plane in a k-dimensional world which can be stored as a q-dimensional datapoints along with eigen vectors and values indicating how much we have lost.

Image recognition example §